WEEK 8

 

6.2 Perimeter, area and volume

6..2.1 Understand the concept of perimeter (2)
6..2.2 Understand the concept of area (1)

Each of this week's tasks involves a fairly simple shape: the rectangle. However, the rectangles are dynamic: they can change in a variety of ways, and we consider what happens to the perimeter as they do. We also start to look at area.

Monday: Here we consider a rectangle ABCD with a vertex, C, that moves on a slanting line. Students might notice that as C moves down the line, the rectangle's height decreases and its width increases, but they do so at different rates. What does this mean for the length of the perimeter?

 

The rectangle shown in the diagram has a perimeter of 26 units. Here C has coordinates (3, 10) and students might notice that the perimeter, 26, is twice the sum of the coordinates, or, more generally that the perimeter = 2(x+y) where C has coordinates (x, y). Some students might also notice that as the x-coordinate of C increases by 1, the y-coordinate decreases by 2 and that therefore the perimeter decreases by 2. We can use this to deduce that as the rectangle has a perimeter of 26 units when the x-coordinate of C is 3, it will have a perimeter of 20 units when the x-coordinate is 3+3=6, ie when C has coordinates (6, 4). A further increase of 0.5 in the x-coordinate of C will produce a rectangle with perimeter 19 units.

It is unlikely that students will use such ideas to the full, but some of the ideas might emerge if students adopt an empirical approach that is systematic.

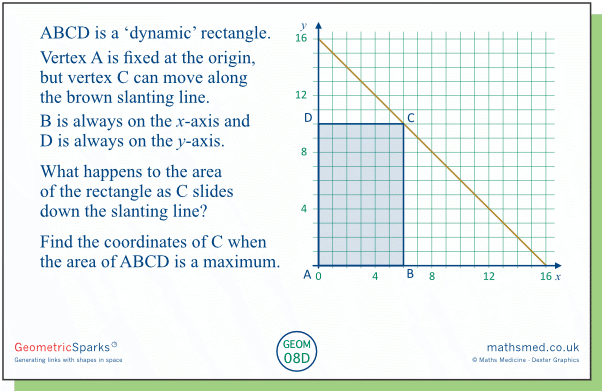
Tuesday: Here we look at the same scenario but this time consider the area of the rectangle rather than its perimeter. We discovered from Monday's task that the perimeter steadily decreases as point C moves down the slanting line. The rectangle's area behaves differently: initially it increases before decreasing again, so at some point it reaches a maximum.

It is unlikely that students will adopt anything other than an empirical approach for finding the maximum area. This happens when C has coordinates (4, 8), which gives an area of 32 square units. An ordered table of values can be useful here, to arrive at this maximum and to reveal that the values of the area are symmetrical about x = 4.

Should we be surprised that this maximum value for the area occurs at this halfway point in C's journey? Not really (though I was at first...).

Wednesday: This is similar to Monday's task, but this time the slanting line is at 45˚ to the axes. (It is symmetrical about y=x; its equation is x+y=16 rather than 2x+y=16). 

It turns out that the perimeter is constant this time, as C slides down the slanting line. This might come as a surprise - at first!

Thursday: Here we look at area again, and discover that it again changes, even though the perimeter is constant.

 

The maximum area occurs at the midpoint of C's journey again, which should come as a no surprise this time - where else could it be, given that we have a 'symmetrical' line (x+y=16) and a symmetrical area relation (area = xy)? This helps to explain why Tuesday's maximum also occurred at the midpoint of C's journey. We can think of Tuesday's diagram as a vertically stretched version of today's, with a scale factor of ×2. This means that for a given value of the x-coordinate of C, the area of the rectangle in Tuesday's diagram will be twice the area of the corresponding rectangle in today's diagram. And so the maximum area will occur for the same value of x, namely x = 4.

Friday: This is quite a rich task but students might need help making sense of the rather subtle definition of the rectangle. It is important for students to try to visualise the rectangle as vertex C moves along the x-axis - you might want to ask them to describe what they see.
[An animation of the rectangle can be found here.]

When point C is near the origin we get a very thin rectangle. The shape becomes more square as the x-coordinate of C increases, but it then starts to get long and thin in the other direction until it essentially disappears when C is at (16, 0).

 Students might find it helpful to treat the diagonal of a grid square as the (diagonal) unit length, and as the side of the 'diamond-oriented' unit square. So, for example, the rectangle shown in the diagram would have a perimeter of 5+6+5+6 diagonal units, and an area of 5×6 diamond unit squares. It is likely that students will explore the value of the perimeter empirically, perhaps by completing a table of values. By analysing the diagram geometrically, it can be shown that the perimeter is equal to the length of the brown line segment + AD, or 16 + AD diagonal units. This means the perimeter approaches a minimum of 16 diagonal units when C approaches the origin, and steadily increases to approach 32 diagonal units as C approaches (16, 0).

The rectangle's area approaches 0 as the x-coordinate of point C approaches 0 and 16. Between those values, it might be thought that the rectangle would have a maximum area when it is a square. (It is a nice challenge for students to find the coordinates of C for which the rectangle is a square.) However, it turns out that the maximal shape is a half-square, as with the classic Sheep Pen problem (where a farmer constructs a rectangular pen using a given length of fencing and part of a wall). This happens when C is at (8, 0).

An illuminating take on this is to reflect the diagram in the brown line (x + y = 16). We then get a double-rectangle enclosed in a 16-by-16 square. What can we say about its perimeter? When is the area a maximum for such a rectangle?

It is also interesting to explore what happens if C is allowed to move beyond the origin to the left, or beyond (16, 0) to the right. In these positions the direction of AD and BC switches, and it makes sense to regard their lengths as negative now - for example, doing so means that the relation 'perimeter = 16 + AD diagonal units' still holds.