6.1.1 Understand and use angle properties (3)
This week's tasks continue the angle chasing theme, and where again it might help to add auxiliary lines or to transform part of the given figure, for example by a translation or rotation. However, the context no longer involves regular polygons.
Monday:
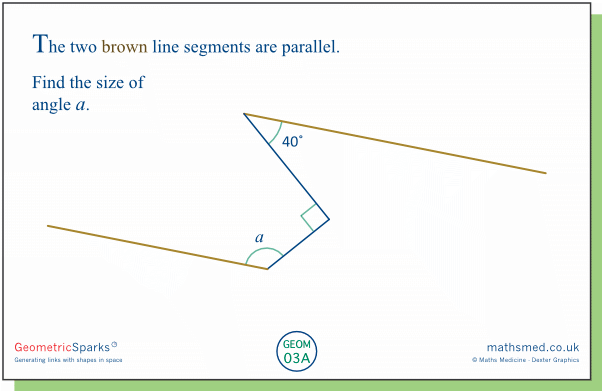
Here we need to use the fact that the brown line segments are parallel. It may take a while for students to spot a way of doing this, as the parallel lines are not connected in the usual, simple way, by a transversal.
The task can be solved in a rich variety of ways. Here are some of the methods that were posted on Twitter:
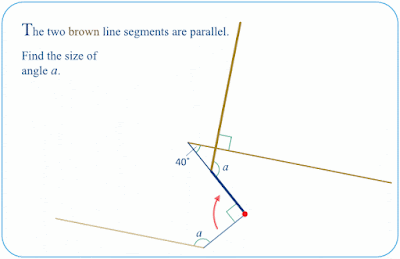
The above methods all involve auxiliary lines. It is also possible to solve the task using transformations, for example a rotation, as here, where the parallel lines become orthogonal:
Tuesday: This task involves a lot of redundant information. It can be made much simpler by, for example, translating the lowest two segments in the diagram such that the purple segments touch or overlap.
Wednesday: Here the redundant part of the diagram in Tuesday's task has been erased. This might help students who struggled with the task to find a solution.
Thursday: This is a classic task that I am particularly fond of (see here). It can be solved in a variety of ways, by adding an auxiliary line or by transforming part of the figure.
Here is an elegant, and perhaps the most common, way of solving the task:
As in the previous task, the size of a is the sum of the two given angles:
