WEEK 2

 

6.1 Geometrical properties

6.1.1 Understand and use angle properties (2)

This week's tasks can be classed as angle chasing tasks, but ones where it might help to add auxiliary lines or to transform part of the given figure, for example by a translation or rotation. They also require knowledge of the interior angles of various regular polygons.

Monday: Here we can make use of the fact that the diagonal of the square makes an angle of 45˚ with the sides of the square, and that the interior angle of a hexagon is 120˚.

A standard, 'static' way to solve this task is to find the size of the angles in the triangle that one can see in the bottom-right of the given diagram. One of these is equal to angle a, one is 45˚ and the other is 180˚–25˚–120˚ = 35˚. So a = 180˚–45˚–35˚ = 100˚.

Another approach is to translate the given diagonal so that it goes through the point where the hexagon touches the square, and then to consider the various angles at that point. (This effectively reduces the earlier triangle to a single point.)
[Note: Rather than translating the diagonal line, we could of course draw an auxiliary line parallel to the diagonal, through the desired point.]

Or we could rotate the hexagon through 25˚ clockwise. This would reduce the size of angle a by 25˚, so it would give us an angle of (a – 25˚) formed by two slanting lines, one at an angle of 45˚ to the horizontal, the other at an angle of 30˚ to the horizontal, giving a – 25˚ = 45˚ + 30˚, and so a = 100˚.

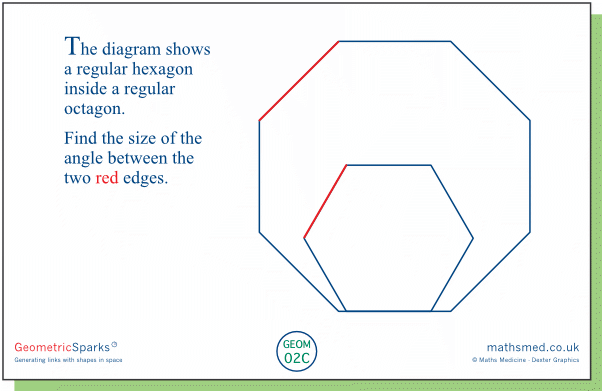
Tuesday: Here we can make use of the fact that the interior angles of the hexagon and octagon are 120˚ and 135˚ respectively, and that the long slanting line bisects the bottom-left interior angle of the hexagon. 

The base of the hexagon sits on the base of the octagon, but none of their vertices coincide. However, we can rectify this by translating the octagon a small distance to the right, so that the bottom-left vertices of the two polygons coincide, and without affecting the size of angle a. This gives a host of angles at this common vertex, one of which is equal to a, and where the rest are known. In turn we can state that a = 145˚–120˚+60˚ = 85˚.

 

Wednesday: Here we again have interior angles of 120˚ and 135˚. Indeed, the red edges make angles of 120˚ and 135˚ with the top horizontal edge of their respective polygons. This allows us to conclude that the angle between them is 135˚ – 120˚ = 15˚. Some students might find this last step hard to visualise and might find it helpful to imagine translating one of the hexagons so that their top-left vertices coincide. In the process, the two red edges meet without changing their orientation and thus form the angle we are looking for.

Here are a two responses that were posted on Twitter. In the first, the red edge of the hexagon has been translated (or an auxiliary line drawn) to pass through a vertex at one end of the other red edge. In the second response, the two red edges have been produced to show the 'actual' angle between them, and to form a triangle from which the size of the angle can be calculated. (The auxiliary line parallel to one of the red edges seems to be redundant.)

Thursday: Here the two red edges are almost parallel, which might add an extra degree of challenge to the task for some students. If we extended the red edges, would they meet to the left and above, or to the right and below?

It turns out that the task has a simple solution, though it may take some time to spot it! The red edge of the octagon is at an angle of 135˚ to the vertical. The other red edge is at an angle of 120˚+20˚ to the vertical. So the (acute) angle between them is 140˚–135˚ = 5˚. Some students might find it easier to visualise the desired angle by bringing the red edges together, for example by translating the hexagon horizontally to the left, until the red edges touch at their top-left ends.

We could also solve the task using a rotation, though this may not be so efficient. For example, we could start by rotating the hexagon anticlockwise through 20˚ (so the polygons touch edge-to-edge) or through 10˚ clockwise (so that its base is horizontal).

Friday: This is a fairly simply variant of Thursday's task. If the red edges are parallel, they both make an angle of 135˚ with the vertical. So a + 120˚ = 135˚.