6..3.1 Understand and use translations (1)
6..3.2 Understand and use rotations (5)
6..3.3 Understand and use reflections (5)
6..3.4 Understand and use enlargements (2)
This
is the final week of transformation tasks, mostly involving reflection
and rotation. It can be thought of as a fairly demanding miscellaneous
exercise.
Monday: The object being transformed (mapped) in this task is symmetrical, so we need to know the image of specific points to be able to determine the transformation.
In part i., we are told that vertex A is mapped onto vertex Y. The only single transformation that will do this, and map the whole blue rectangle onto the brown rectangle, is a rotation. This means B is mapped onto Z, C onto W and D onto X. How readily do students recognise that this is what happens?
A very grounded way of finding the centre of rotation here is to extend the blue line segment AB and the brown line segment YZ and to think about the corresponding points that this generates. The most significant pair of these occurs where the extended lines meet: since corresponding points coincide here, it must be the centre of rotation!
In part ii., we are told that vertex A is mapped onto vertex W. Again, the only single transformation that will do this, and map the whole blue rectangle onto the brown rectangle, is a rotation. This time B is mapped onto X, C onto Y and D onto Z.
It is an interesting challenge to try to find the centre using the grounded approach described for part i. However, it is not an efficient method for this task and is likely to involve several steps before corresponding points are found that coincide. An example of the method is shown below, where we can see that H (or H') is the centre.
Tuesday: It looks as though the transformation here is an enlargement, though we cannot be sure as none of the vertices of the object and image are grid points.
The construction lines drawn through corresponding points, shown in the diagram below, seem to meet at a single point, which suggests that the transformation is indeed an enlargement. An effective way to then find the scale factor is to compare the widths of the two shapes as the shapes seem to be a whole number of units wide, namely 2 and 7. This means the scale factor is 3½.
Wednesday: In this task we are shown only part of the image resulting from a transformation. From what we can see, the transformation could be a translation or a reflection.
A translation of 4 units across and 2 up will take E to E'. When this is applied to the rest of the plane, including G, then G' will have coordinates (1+4, 5+2), or (5, 7). The image of EFG under the translation is shown by the brown lines, below.
If EF is reflected onto E'F', the mirror line will bisect and be perpendicular to the line segment EE'. The point on the mirror line closest to point G has coordinates (7, 8) and is 6 units across and 3 units up from G. So G' will have coordinates (7+6, 8+3), or (13, 11). The image of EFG under the reflection is shown by the heavy green lines, below.
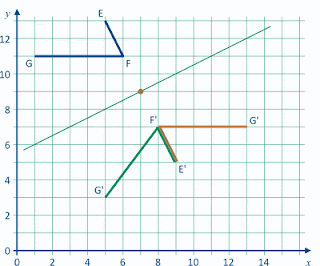
Thursday: In this task we are shown only part of the image resulting from a
transformation. From what we can see, the transformation could be a rotation or a reflection.
A rotation of 180˚, with the centre at (7, 9) will map EF onto E'F'. The centre is 6 units across and 2 units down from G, so G' will have coordinates (7+6, 9–2), or (13, 7). We can also find G' by using the fact that F'G' will be horizontal (Why?) and G' will be 5 units from F'. The image of EFG under the rotation is shown by the brown lines, below.
If EF is reflected onto E'F', the mirror line will bisect and be
perpendicular to the line segment FF'. The point on the mirror line
closest to point G has coordinates (3, 7) and is 2 units across and 4 units down from G. So G' will have coordinates (3+2, 7–4), or (5, 3). The image of EFG under the reflection is shown by the heavy green lines, below.
Friday: In this task we are shown only part of the image resulting from a
transformation. From what we can see, the transformation could be a rotation or a reflection.
It may take a while for students to see that the centre of rotation that maps FE onto F'E' will be at (7, 5), even though this point is at the intersection of EF and E'F' produced. The line segments EF and E'F' are at 90˚ so the image of the horizontal segment FG will be vertical. This means G' will be 6 units above F' with coordinates (9, 6+5), or (9, 11). The image of EFG under the rotation
is shown by the brown lines, below.
If EF is reflected onto E'F', the mirror line will bisect and be
perpendicular to the line segment FF'. The point on the mirror line
closest to point G has coordinates (7, 5) and is 6 units across and 2
units down from G. So G' will have coordinates (7+6, 5–2), or (13, 3). The
image of EFG under the reflection is shown by the heavy green lines,
below.