6..2.2 Understand the concept of area (3)
Here we take a step backwards, perhaps, to visit a fundamental idea about area. When we consider the amount of 2-dimensional space covered by a region, we are not restricted to measuring this area in unit squares: any congruent shapes that cover space uniformly can be used. We can even use regularly distributed marks, such as small dots, to compare areas.
Monday: Here we compare areas by seeing how many of the evenly distributed dots are enclosed by each shape. The smaller shape contains 15 dots (or perhaps 16, depending on whether we include dots on, or partly on, the edge). The larger shape contains 135 (or perhaps 136) dots, so about 9 times as many. Some students might be surprised that the factor is 9 rather than 3, but of course it confirms the fact that a (linear) scale factor of 3 results in an area factor of 3² = 9. Can students see why?
Before students start counting dots, you might want to ask for some estimates of how much larger the area of the larger shape is than the area of the smaller shape. Do some students say 3? Do some say 9, and if so why? (Do they give a numerical explanation, along the lines of 9 = 3², or a visual/structural explanation, such as seeing a 3 by 3 array of the smaller shape?) Do any give an intermediate value, such as 5 or 6?
Tuesday: Here we measure area in unit parallelograms. An efficient way to estimate the scale factor is to use the fact that the shapes are about 4 and 10 grid-spaces wide. So the scale factor is about 2.5 (and, as we shall see, the area factor is about 6 [or 6.25]).
When it comes to counting the small parallelograms, some students might decide to include only those that are at least half inside a shape. Others might decide to match up partially covered parallelograms to make roughly whole parallelograms. Using the latter approach, the two shapes cover about 10 and 61 or 62 parallelograms respectively. Again, some students might be surprised that the linear and area scale factors are not the same.
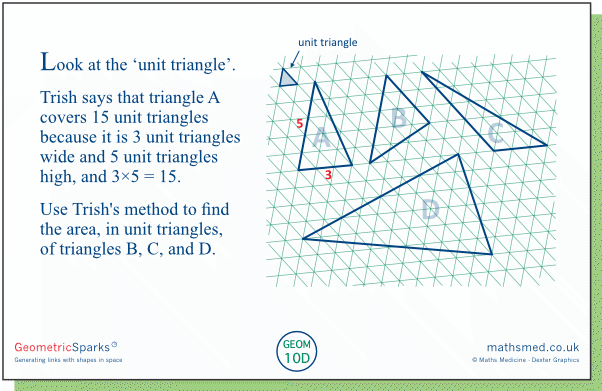
Wednesday: Here we measure area in 'unit triangles'. Using Trish's methods, the triangles' areas, in unit triangles, come to 15, 4×3=12, 5×5=25, 8×4=32 and 3×5=15. Students might be unsure about how to measure triangle E. One way is to transform it into triangle A by moving the top vertex parallel to the 'horizontal' base.

Students can confirm that Trish's method seems to work by counting triangles, though this is not straightforward and it doesn't provide a mathematical proof. The diagram below shows the basis of a proof. Here two copies of a triangle are arranged to make a parallelogram, in this case consisting of 3 columns of 5 small parallelograms, making 3×5=15 small parallelograms in all, each consisting of 2 unit triangles....
[Note: We can describe
triangle A as having a 'base' of 3 units and a 'height' of 5 units.
However, the units here are different! Each refers to the length of the
corresponding side of the unit triangle.]
Thursday: Here we measure area in 'unit triangles' again, but this time we apply Trish's method to triangles where perhaps none or only one of the edges is parallel to any of the edges of the unit triangle.
Triangle A is the same as before and has an area, in unit triangles, of 3×5=15.
We can think of triangle B as having an almost vertical base of 5 and an almost horizontal height of 3, so it too has an area of 15 unit triangles. Some students might notice that we can transform B into A by sliding the rightmost vertex 'down' 2 units, parallel to the side of 5 units.
Triangle C has a base of 3 units and a height of 5 units, like triangle A. We can make this clearer by transforming it into triangle A, by sliding its topmost vertex to the 'right'.
Triangle D is more challenging. One way to find its area is to partition it into two triangles along a 'horizontal' line through the leftmost vertex. This gives two triangles with a shared base of 10 units and heights of 2 and 4 units, making a total area of 10×(2+4)=60 unit triangles.
Friday: Here we measure the area of identical yellow triangles in unit squares and in unit triangles. A close examination of the grids on which the triangles are drawn, shows that the gap between the horizontal lines is the same for both grids, as is the horizontal distance between the vertical lines and between the slanting lines. Because of this, two unit triangles can be put together to make a parallelogram with the same base and height as the unit square.
The area of the yellow triangle is ½×5×4 = 10 unit squares and 5×4 = 20 unit triangles. This makes sense, since two unit triangles have the same area as one unit square.