6.1.2 Understand and use similarity and congruence (2)
Monday: Here we have two angles which look more or less the same. How can one tell which is larger?
This is a challenging task and one shouldn't be too concerned if after a while students give up or resort to using a protractor. However, the task gives students the opportunity to explore the affordances offered by the square grid: where line segments go through grid points, the grid allows one to compare the slope of lines; however it is often not so easy to compare lengths just by inspection (though very easy using Pythagoras' rule - see Week 6); and, as in this task, the grid is often not helpful when inspecting the angle between slanting lines (unless the lines are at right angles).
One way to make constructive use of the given grid is to consider the grid point P and its image P' when reflected in AC. (Note that AC has a slope of 3 forwards, 1 up and PP' has a slope of 1 back, 3 up.) Angle BAC = angle P'AC and, as we can see, angle P'AC is slightly less than angle DAC.
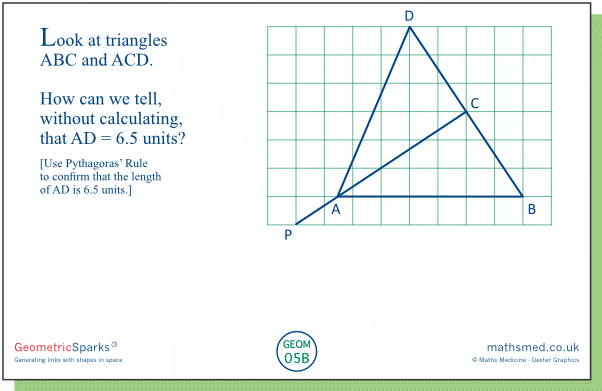
Tuesday: Here we have two congruent triangles. (Why?) So AD = AB = 6.5 units.
Most students will probably accept that the triangles look the same, but it is quite a different matter to marshal an argument that this is the case and to find the relevant facts to support it. The triangles can be shown to be congruent on the basis of SAS (two pairs of equal corresponding sides and an equal angle between them). The triangles share the side AC; also BC = DC, which we can see directly from the grid; finally, the interior angles at C are equal as they are right angles, which we can tell from the slopes of BD (2 back, 3 up) and AC (3 forwards, 2 up).
We can also find the length of AD by applying Pythagoras' Rule to the right angled triangle AED, where E is the point on AB directly below D. The arms of this triangle are 2.5 and 6 units long, so AD² = 2.5² + 6², which eventually leads to AD = 6.5. Another way of approaching this is to think of the right angled triangle that is twice the size of AED, which gives us the (familiar?) Pythagorean triple 5, 12, 13.
Wednesday: It is relatively easy to cut a square into 4 congruent pieces. For example, any pair of orthogonal lines through the centre of the square will do it. What other ways might there be?
This task provides plenty of scope for exploration. Students may discover that only some of the dissections that work for a square also work for a rectangle, and that only some of those that work for a rectangle also work for a parallelogram.
Thursday: The shape of a triangle is uniquely defined if its 3 angles are known. Its shape and size are uniquely defined if we also know the length of one side, or if we just know the length of three sides, or two sides and the included angle, or if the triangle is right-angled and we know the length of the hypotenuse and another side. Things are a lot looser for quadrilaterals. Here we explore what we know about the shape of a quadrilateral when we know the length of its 4 sides.
These are the solutions for questions 1, 2 and 3:
These are the solutions for questions 1, 2 and 3: